Leading with leaders

——WGCNA代码

WGCNA其译为加权基因共表达网络分析。该分析方法旨在寻找协同表达的基因模块(module)，并探索基因网络与关注的表型之间的关联关系，以及网络中的核心基因。WGCNA适用于复杂的数据模式，推荐5组(或者15个样品)以上的数据。一般可应用的研究方向有：不同器官或组织类型发育调控、同一组织不同发育调控、非生物胁迫不同时间点应答、病原菌侵染后不同时间点应答。

基本原理

从方法上来讲，WGCNA分为表达量聚类分析和表型关联两部分，主要包括基因之间相关系数计算、基因模块的确定、共表达网络、模块与性状关联四个步骤。

第一步计算任意两个基因之间的相关系数（Person Coefficient）。为了衡量两个基因是否具有相似表达模式，一般需要设置阈值来筛选，高于阈值的则认为是相似的。但是这样如果将阈值设为0.8，那么很难说明0.8和0.79两个是有显著差别的。因此，WGCNA分析时采用相关系数加权值，即对基因相关系数取N次幂，使得网络中的基因之间的连接服从无尺度网络分布(scale-freenetworks)，这种算法更具生物学意义。

第二步通过基因之间的相关系数构建分层聚类树，聚类树的不同分支代表不同的基因模块，不同颜色代表不同的模块。基于基因的加权相关系数，将基因按照表达模式进行分类，将模式相似的基因归为一个模块。这样就可以将几万个基因通过基因表达模式被分成了几十个模块，是一个提取归纳信息的过程。

WGCNA术语解读

权重(weghted)：

基因之间不仅仅是相关与否，还记录着它们的相关性数值，数值就是基因之间的联系的权重(相关性)。

模块（Module）：

表达模式相似的基因分为一类，这样的一类基因成为模块；

Eigengene：

Eigengene（eigen- +‎ gene）：基因和样本构成的矩阵，https://en.wiktionary.org/wiki/eigengene

邻接矩阵（Adjacency Matrix）：

是图的一种存储形式，用一个一维数组存放图中所有顶点数据；用一个二维数组存放顶点间关系（边或弧）的数据，这个二维数组称为邻接矩阵；在WGCNA分析里面指的是基因与基因之间的相关性系数矩阵。 如果用了阈值来判断基因相关与否，那么这个邻近矩阵就是0/1矩阵，只记录基因相关与否。但是WGCNA没有用阈值来卡基因的相关性，而是记录了所有基因之间的相关性。

Topological Overlap Matrix (TOM)：

WGCNA认为基因之间的简单的相关性不足以计算共表达，所以它利用上面的邻近矩阵，又计算了一个新的邻近矩阵。一般来说，TOM就是WGCNA分析的最终结果，后续的只是对TOM的下游注释。

数据要求：

   表达谱芯片或测序数据（已经过预处理）

下游分析

得到模块之后的分析有：

1.模块的功能富集

2.模块与性状之间的相关性

3.模块与样本间的相关系数

挖掘模块的关键信息：

1.找到模块的核心基因

2.利用关系预测基因功能

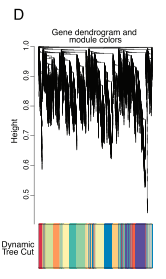
图形示例：

1、使用加权的表达相关性对基因的表达数据进行共表达分析，并构建共表达网络。接着基于加权相关性，进行层级聚类分析，并根据设定标准切分聚类结果，获得不同的基因模块，用聚类树的分枝和不同颜色表示不同模块

图注：

上方树状图代表各基因加权相关性关系，下方色区代表对应颜色的基因模块，左侧标尺代表基因之间的关联距离。

2、模块互作关系分析

根据基因间表达量进行聚类分析，得到的各模块间的相关性图

图注：上方树状图代表模块聚类，下方热图为模块间的相关性热图

3、导出TOM矩阵，绘制相关性图

WGNA认为基因之间的简单的相关性不足以计算共表达，所以它把邻接矩阵转换为拓扑重叠矩阵，以降低噪音和假相关，获得的新距离矩阵（Topological Overlap Matrix，TOM）

图注：树状图代表RNA表达量聚类，左轴及上轴色块代表标注对应颜色的基因模块，热图为各基因的的TOM信息，可以明显看到不同模块中不同RNA聚类的表达差异。

应用示例：

文献1:眼中葡萄膜黑色素恶性瘤基因共表达网络分析（眼癌中共表达网络分析及关键biomarker查找）于2018年1月发表在Exp Eye Res. ，影响因子2.998

主要的分析思路其实就是WGCNA的分析思路：

文献2:胃癌中miRNA共表达网络分析（胃癌中共表达网络分析及关键biomarker查找

）也是一篇WGCNA分析的文章，只是换了换癌种以及分析的基因变成了miRNA，分析思路几乎与上篇文章一致。可以查看原文；于2016年8月发表在Genomics.，影响因子3.16