- 产品详情
- 产品参数
- 产品评论
比例风险回归模型,又称Cox回归模型,是由英国统计学家D.R.Cox与1972年提出的一种半参数回归模型。模型可以用来描述了不随时间变化的多个特征对于在某一时刻死亡率的影响。它是生存分析中的一个重要的模型。
应用场景
cox比例风险回归模型,由英国统计学家D.R.Cox于1972年提出
主要用于肿瘤和其他慢性疾病的预后分析,也可用于队列研究的病因探索
单因素cox分析主要探索单个基因的独立预后影响
cox分析可用于转录组,甲基化,miRNA, LncRNA, 可变剪切等等
基本原理:

在这里,![]() 是一个与时间有关的基准危险率,其选择具有充分的灵活度,一种可能的选择是采用概率论中的Weibull分布。
是一个与时间有关的基准危险率,其选择具有充分的灵活度,一种可能的选择是采用概率论中的Weibull分布。![]() 是模型的参数。由于只要给定数据,就能够通过极大似然估计求出模型的参数
是模型的参数。由于只要给定数据,就能够通过极大似然估计求出模型的参数![]() ,而
,而![]() 的选择具有很大的灵活性,所以我们称之为一个半参数模型。
的选择具有很大的灵活性,所以我们称之为一个半参数模型。
对公式进行变形,得到:

通过这个公式,我们可以发现,模型中各危险因素对危险率的影响不随时间改变,且与时间无关,同时,对数危险率与各个危险因素呈线性相关。这就是Cox回归中的两个基本假设。
参数的极大似然估计:
术语解读:
1.输入变量,由m个影响因素组成:

2.生存函数,输入为X时,在t时刻仍然存活的概率:
3.死亡函数,输入为X时,在t时刻已经死亡的概率:
4死亡密度函数,输入为X时,在t时刻死去的概率:

5.危险率函数,输入为X时,已经生存到t时刻,而在t时刻死去的概率:

6.风险比(hazard ration,HR)
数据要求:
样本数据中关注的特征信息以及样本的生存时间和生存状态信息。
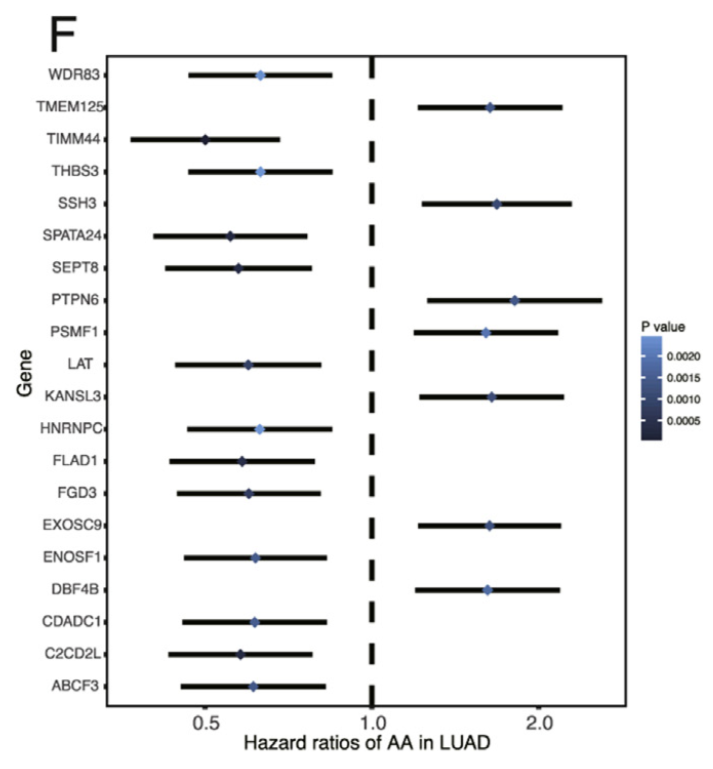
图形示例:


图注:横轴HR,纵轴关注的样本特征
应用示例:于2017年2月发表在cancer letters (影响因子6.508)
各种剪切活动下单元回归分析显著基因,部分结果如图

单因素回归分析:文章中为了研究mRNA剪接事件对预后的影响,首先进行了单变量生存试验,以评估TCGA中LUAD和LUSC数列中临床参数与结果之间的关系。

多因素回归分析:挑选对生存影响最重要的前7种剪切活动作为候选因素。为了去除预后基因模型中非独立影响因素的事件,对备选剪接事件应用具有预后模型构建的多变量Cox回归。